Обективите с които ежедневно снимаме са сложен набор от компоненти. Преобладаващата част компоненти са кръгли на вид ту изпъкнали, ту вдлъбнати стъкълца, благодарение на които проектираме образа пред камерата, върху матрицата или филма намиращ се вътре в камерата. За съжаление все още не е открито перфектното стъкло което да няма никакви загуби на светлина и разбира се никакви грешки в изображението. Съвременните обективи имат малко или още по-малко някакви оптични грешки. Наричат се аберации.
Оптичните грешки се изучават както в нормалните училища (часовете по физика), така и в специализираните технически, както и някои висши учебни заведения. Трябва да се признае, че не е от най-лесните и леко смилаеми материи. В последните години фотографията стана изключително масова и професионалната терминология и начин на обяснение на аберациите значително се опрости, с цел по-лесно обясняване на различните оптични грешки. От една страна това може би е добре, но от друга… получава се нещо като криво разбраната цивилизация.
Днес имаме удоволствието да ви представим една кратка статия за част от аберациите които срещаме в процеса си на снимане. Авторът на статията, г-н Християн Стоянов е дългогодишен преподавател по оптика, запознат от близо с материята. Разговорът ни с него започна покрай една статия, в която с унисон с модерното интернет общество, бяхме избягали от професионалният език, заменяйки го със съвременен буквално преведен фотографски жаргон. Говорейки за за този навлязъл жаргон и за това, че е добре все пак нещата да се казват с правилните имена, се появи идеята и за по-професионална статия за оптичните грешки. Следващите редове са изключително полезни за фотографите които искат да обогатят своите теоретични познания за обективите които използват ежедневно и защо не винаги изображението е такова каквото искаме. Приятно четене.
За оптичното изобразяване
Оптичните аберации на някои езици се наричат още „грешки при изобразяването“. Точно оптично изобразяване се наблюдава, когато светлината, излъчена от светеща точка -наречена предмет, под въздействието на някаква среда (оптична система) се концентрира отново в друга точка – наречена образ. Такъв вид изобразяване се нарича стигматично. В пространството двете точки, за които казваме, че са оптично спрегнати, могат да бъдат разделени, но могат и да се сливат. Вторият случай се нарича само спрягане или само изобразяване. Лесно може да се докаже, че във всяка оптична система съществуват поне една двойки само спрегнати точки. Наричат се точки на Браве (Auguste Bravais) и играят важна роля при конструирането на варио-обективите.
Оптичен път се нарича произведението между геометричния път и показателя на пречупване на средата. Тъй като показателят на пречупване на дадена среда е отношението между скоростите на разпространение на светлината във вакуум и в средата, то оптичният път между две точки е равен на пътя, който би изминала светлината във вакуум за същото време. Съгласно теоремата на Малюс, при стигматично изобразяване оптичният път между две спрегнати точки, измерен по протежение на произволен лъч, е константа.
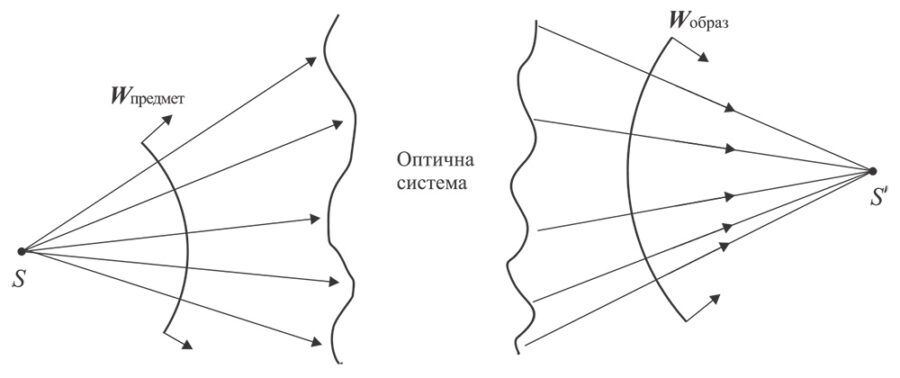
Идеален точков източник излъчва равномерно във всички посоки – изотропен източник. Следователно трептенията, тръгнали едновременно, след известно време ще бъдат наблюдавани с еднаква фаза върху сферична повърхност – сферичен вълнов фронт. Но тогава това би означавало, че при стигматично изобразяване влизащият в оптичната система сферичен вълнов фронт се трансформира в друг такъв, с център в образната точка.
Следователно, при стигматично изобразяване сферичен фронт (W предмет), с център в предметната точка, се трансформира в сферичен фронт (W образ), с център в образната точка. Инструменталните оптични системи традиционно съдържат елементи с плоски или сферични повърхности. Това се е наложило от чисто практични (технологични) съображения. Дълги години при тези форми по-лесно се постигала желаната точност. И при най-простата оптична система – сферична граница между две среди, лесно може да се докаже, че теоремата на Малюс не е удовлетворена. Нека си припомним, че в параксиалната оптика се дефинира фундаменталното понятие зеници на оптичната система. Те са винаги две – входна и изходна и са образи на основната (механична) апертурна бленда, съответно с всички елементи преди и зад нея. Зениците определят колко енергия ще протече през системата. Но също така положението на зениците до голяма степен определя и аберационното състояние на системата.
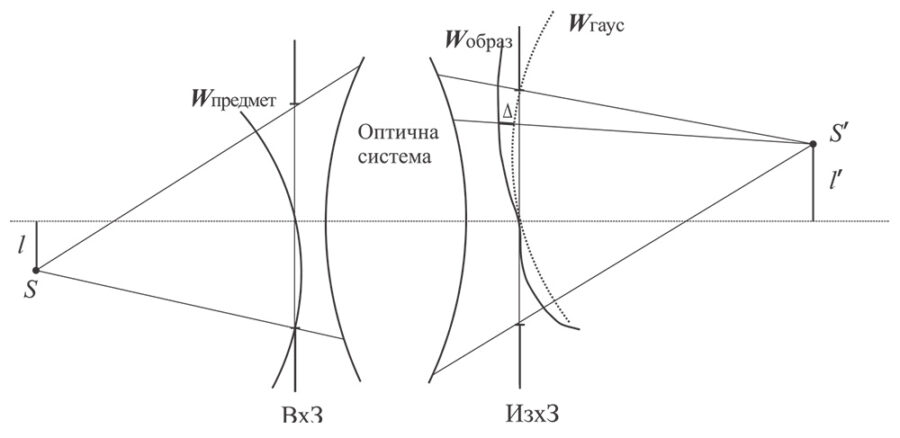
При изобразяване на предметна точка S на изхода на реална оптична система вместо идеална сферична вълна (W гаус), с център в очаквания идеален параксиален образ, се наблюдава вълнов фронт (W образ) с друга форма. Нека мислено построим разликата Δ в оптичните пътища между двата вълнови фронта – реален (W образ) и идеален сферичен (W гаус, нарича се гаусова опорна сфера), разлика, измерена по протежение на всеки от лъчите. Разпределението на тази разлика по апертурата на системата се нарича вълнова аберация.
Това е единствената аберация, реално съществуваща и измерима. В миналото хората са се досетили да подложат вълновата аберация на математичен анализ. Разложили я в степенен ред по три подходящо подбрани променливи (наричат се зайделови променливи и имат ясен оптичен смисъл). Оказало се, че коефициентите пред четните степени на този ред са равни на нула. Нулевият член в това развитие описва степента на дефокусировка. Следващите пет члена (с максимална трета степен на променливите) описват петте основни монохроматични аберации: сферична аберация, кома, астигматизъм, кривина на полето, дисторсия. Те никога не съществуват самостоятелно. Но така изразени, те имат много ясен, нагледен оптичен смисъл. Лесни са за тълкуване, разбираеми са за конструктора. Всяка промяна в оптичните параметри на системата води непосредствено до промяна в стойностите на коефициентите в тези пет члена от трети ред – в корекционното състояние на оптичната система.
Забележка: Не бива да забравяме, че цялото това разглеждане е възможно само за един цвят – за една дължина на вълната. Но това не е беда. Науката за спектрите ни дават възможност да разложим светлината на плътен набор (спектър) от честоти, мислено да ги пропуснем една по една да ги пропуснем през оптичната система и на изхода резултатите да суперпонираме. И така да получим реалното образно поле. Ако отделните монохроматични образи съвпаднат ще получим верен, „бял“ образ. Но ако те са разместени в пространството, казваме че оптичната система е натоварена с цветна (хроматична) аберация.
Основните монохроматични аберации
За по-добра нагледност ще разгледаме само петте основни монохроматични аберации. Не бива да се забравя, че освен тях в изграждането на образа участват всички членове в развитието на вълновата аберация – от пети, седми и по-горен ред. Съществува едно правило, че ако аберациите от трети ред са много малки, то и тези от по-горен ред също са малки. Но това не е задължително вярно винаги. С подходящ подбор на материалите, радиусите на кривина, дебелините на лещите и разстоянията между тях, аберациите могат да бъдат редуцирани до степен, приемлива за дадена цел. Този процес се нарича корекция на аберациите.
Сферична аберация
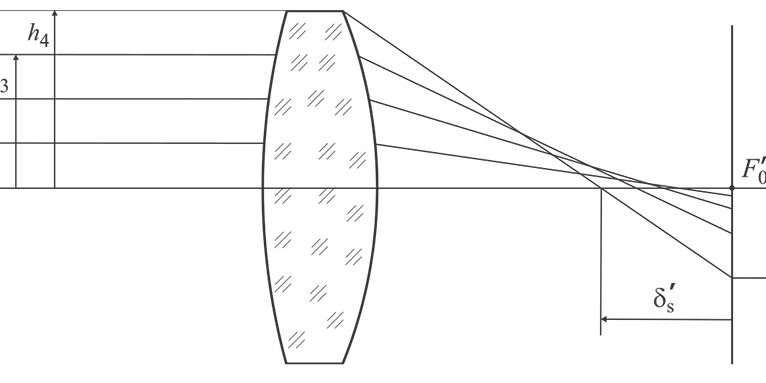
Нарича се така, защото първоначално е била установена като типично свойство на сферичните повърхнини. Но тя се наблюдава и при някои асферични повърхнини. Смисълът на тази аберация става ясен от следната фигура.
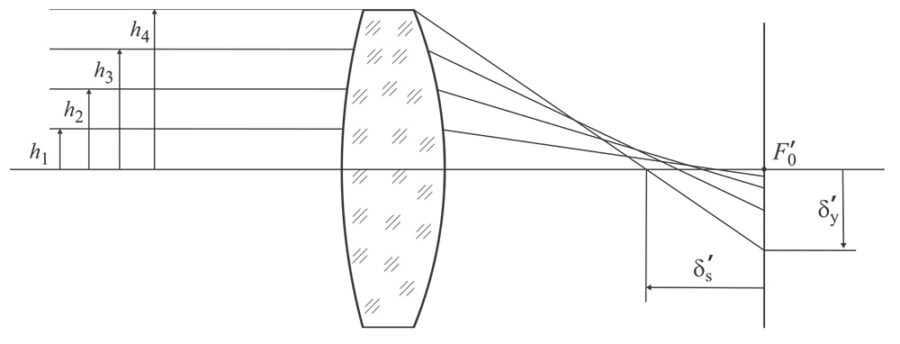
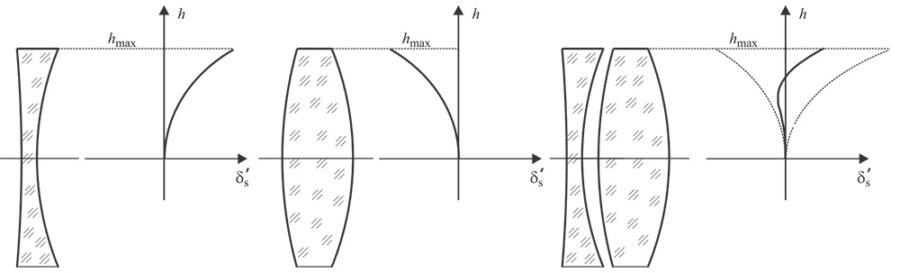
Разглеждаме изобразяването на осева точка с широк сноп (за простота – източникът е в безкрайност). С нарастване на височината h на падане на лъча върху сферичната повърхнина, пресечната му точка с оптичната ос се отдалечава от параксиалната образна точка. В резултата на този процес в параксиалната образна равнина (но в съседните, успоредни на нея) се наблюдава кръгче вместо точков образ. При това разпределението на интензитета на светлината по радиуса на кръгчето не е равномерно. За количествена оценка на сферичната аберация се дава зависимостта δ\’y = ƒ (h) (напречна сферична аберация) или зависимостта δ\’s = ƒ (h) (надлъжна сферична аберация).
От горната фигура се вижда, че при положителна или отрицателна оптична сила на елемента се наблюдава сферична аберация с противоположен знак. Същото важи както за отделни лещи, така и за съставни оптични системи. Следователно при подходяща комбинация на две лещи (или системи) с противоположна оптична сила (положителна и отрицателна) може да се постигне известна степен на корекция на сферичната аберация.
Кома
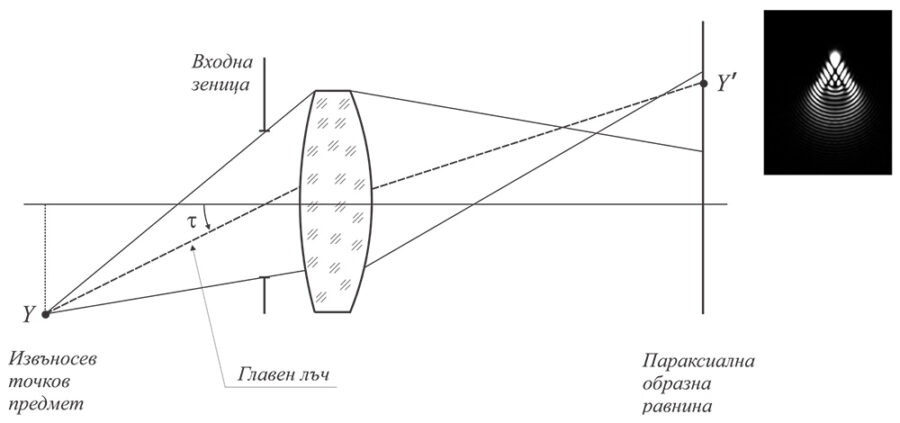
При изобразяване на извъносев точков източник с широк сноп се наблюдава аберацията кома.
Образът на точка Y е удължено петънце с формата на запетайка (от английски, а някои свързват този термин с вида на комета). Причината за появата на този ефект е различният ъгъл на падане за двата крайни лъча от коничния сноп, определен от предметната точка и контура на входната зеница и, с който се осъществява изобразяването.
Количествено стойността на комата се изразява с разстоянието между главният лъч на снопа и крайните лъчи, измерени между съответните пресечни точки с параксиалната образна равнина. При това, тези разстояния се измерват в две ортогонални равнини – тангенциална (меридионална) и сагитална. Стойността на комата нараства пропорционално на зрителния ъгъл τ и с квадрата на относителния отвор. Както забелязваме, процесът е подобен на предишния. За това понякога комата се нарича сферична аберация на наклонените снопове.
Астигматизъм кривина на полето
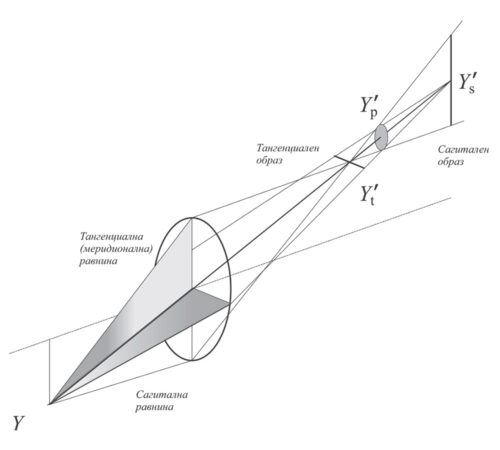
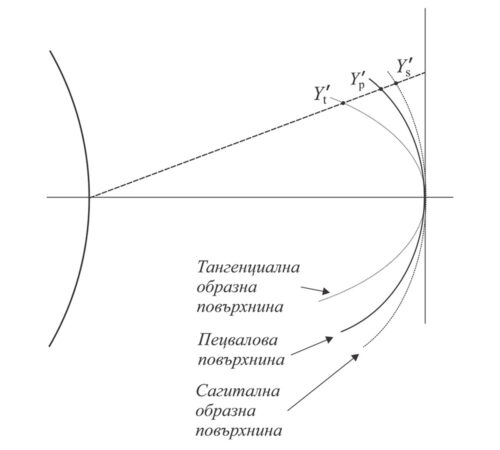
Ако при изобразяването на извъносева предметна точка Y започнем да намаляваме диаметъра на снопа (казано по-просто „да затваряме блендата“), комата ще дегенерира в астигматизъм. Астигматизмът е кома на безкрайно тесните снопове. Тази аберация е свойство на оптичните повърхнини и не може да бъде отстранен напълно. Астигматизмът се проявява в това, че крайните лъчи на снопа се пресичат в тангенциалната равнина в образната точка Y\’t, а в сагиталната равнина в друга точка Y’s, отместена в пространството спрямо първата. Крайните лъчи на снопа формират сложна повърхнина. Лъчите, лежащи във всяка от основните равнини – тангенциална и сагитална, се събират в две ортогонални отсечки с центрове в точките Y’t и Y’s съответно. По средата между тях има сечение във формата на кръгче. По тази причина понякога казваме, че далечна звезда се вижда като точка с лъчи. Геометричното място на тангенциалните и сагитални образи покриват съответно тангенциалната и сагитална образна повърхнина, а между тях, там където са кръговите сечения, лежи образната повърхнина (по-точно там се стремим да разположим чувствителния слой на филма или матрицата).
Следователно, благодарение на астигматизма, предметната равнина се трансформира в закривена повърхност. Тя се нарича пецвалова повърхнина, а нейната кривина, измерена на оптичната ос, се нарича пецвалова кривина или кривина на полето. Във филмовата ера имаше държавни стандарти, които регламентираха натиска и деформацията на филмовата лента така, че огънатия чувствителен слой максимално да съвпада с пецваловата повърхнина.
Астигматизмът и кривината на полето нарастват с втората степен на зрителния ъгъл τ. При малки стойности на зрителния ъгъл (например при телеобективите), намаляване на кривината на полето се постига, ако е спазено условието на Пецвал
(1/n1ƒ’1) + (1/n2ƒ’2) + (1/n3ƒ’3) + … =0
Дисторсия
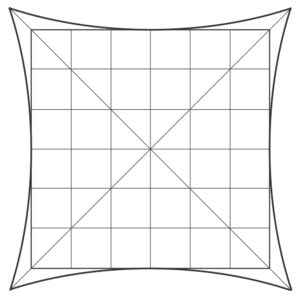
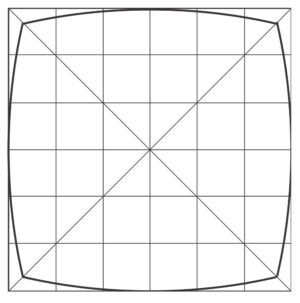
Причината за поява на дисторсия е изменението на напречното увеличение с нарастването на зрителния ъгъл τ. А тази промяна от една страна е причинена от сферичната аберация в зениците, а от друга от отклонението на стойността на ъгловото увеличение от +1. При наличието на дисторсия казваме, че е нарушена ортоскопичността на системата – степента на подобие между образа и предмета. В този случай образът на права линия, лежаща в предметна равнина, е крива. Количествено дисторсията се изразява в относителното изменение (най-често в проценти) на големината на образа в зависимост от зрителния ъгъл τ. За разлика от останалите аберации, дисторсията не влияе върху остротата на образа. И също така, за разлика от останалите аберации , тя може да бъде отстранена напълно. Оптични системи с нулева дисторсия се наричат ортоскопични.
Такива са симетричните (спрямо равнината на апертурната бленда) оптични системи с напречно увеличение -1. Ако увеличението има друга стойност, то на тази стойност трябва да се равнява отношението на фокалните разстояния на двете половини на системата, разделена с равнината на апертурната бленда. Промяната на мястото на апертурната бленда силно изменя стойността на дисторсията и комата. Ортоскопични са фотограметричните обективи, тези за копиране на шаблоните на интегрални схеми, някои висококачествени копирни обективи и др.
Дисторсия
Причината за поява на дисторсия е изменението на напречното увеличение с нарастването на зрителния ъгъл τ. А тази промяна от една страна е причинена от сферичната аберация в зениците, а от друга от отклонението на стойността на ъгловото увеличение от +1. При наличието на дисторсия казваме, че е нарушена ортоскопичността на системата – степента на подобие между образа и предмета. В този случай образът на права линия, лежаща в предметна равнина, е крива. Количествено дисторсията се изразява в относителното изменение (най-често в проценти) на големината на образа в зависимост от зрителния ъгъл τ. За разлика от останалите аберации, дисторсията не влияе върху остротата на образа. И също така, за разлика от останалите аберации , тя може да бъде отстранена напълно. Оптични системи с нулева дисторсия се наричат ортоскопични.

Такива са симетричните (спрямо равнината на апертурната бленда) оптични системи с напречно увеличение -1. Ако увеличението има друга стойност, то на тази стойност трябва да се равнява отношението на фокалните разстояния на двете половини на системата, разделена с равнината на апертурната бленда. Промяната на мястото на апертурната бленда силно изменя стойността на дисторсията и комата. Ортоскопични са фотограметричните обективи, тези за копиране на шаблоните на интегрални схеми, някои висококачествени копирни обективи и др.
Екипът на Фото кафе благодари на г-н Християн Стоянов за гостуването му.